정렬 알고리즘의 종류와 시간복잡도를 이전 글에 포스팅을 했고 이번에는 복잡하지만 효율적 정렬 알고리즘을 구현해보았다.
[정렬 알고리즘의 종류와 시간복잡도]
정렬 알고리즘 시간 복잡도, 공간 복잡도와 구현
정렬 알고리즘의 종류와 시간복잡도 백준 알고리즘에서 실버단계로 올라가면서 점점 알고리즘을 공부해야 한다는 필요성을 느꼈다. 그래서 가장 기본적인 정렬알고리즘에 대해 정리를 해보고
rnflajdrnfl.tistory.com
이번 블로그에서는 복잡하지만 효율적 정렬을구현을 해보았다. 시간복잡도(nlogn)
사용한 프로그래밍 언어는 c#입니다.
쉘 정렬( shell sort )
삽입 정렬 알고리즘의 작동원리는 배열의 특정 인덱스값이 정렬된 배열과 비교되어 알맞는 자리에 삽입을 하는 과정입니다. 만약 특정 인덱스 값이 삽입되어야 하는 자리에서 멀다면 정렬된 배열과 비교를 하는데 시간이 많이 소요됩니다. 이런 시간의 낭비를 줄이기 위해 확장되어 나온 알고리즘이 쉘 정렬 알고리즘입니다.
쉘 정렬 알고리즘의 기본 개념은 원래 배열을 작은 배열로 나누고(이때 갭 시퀀스를 사용해 배열을 나눈다) 삽입 정렬 알고리즘을 사용하여 작은 배열들을 정렬하는 것입니다. 작은 배열의 사이즈를 서서히 줄임으로써 표준 삽입 정렬 알고리즘보다 효율적인 방법으로 원래의 배열를 정렬할 수 있습니다.
시간 복잡도:O(n log n), 공간복잡도: O(1)
쉘 정렬 알고리즘 작동원리
- 갭 시퀀스를 정의합니다. 이 갭 시퀀스는 어레이 크기를 2로 나눈 값에서 시작하여 1이 될 때까지 반 토막이 납니다.
- 간격 시퀀스의 첫 번째 요소와 동일한 간격 크기를 가진 하위 배열에 삽입 정렬을 수행합니다.
- 갭 크기를 갭 시퀀스의 다음 요소로 줄이고 2단계를 반복합니다.
- 간격 크기를 줄이고 간격 크기가 1이 될 때까지 2단계를 반복합니다.
- 마지막으로 어레이 전체에서 삽입 정렬을 수행하여 모든 요소가 올바른 순서로 되어 있는지 확인합니다.
쉘 정렬 알고리즘 예시
쉘 정렬에 대한 예시는 다음 블로그에서 자세한 설명이 나와있으므로 참고해보세요! 저도 이 블로그 보고 이해 했습니다.
[알고리즘] 셸 정렬(shell sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
백준예제문제
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
구현
//셸 정렬 (성공)
using System.Text;
class MainApp
{
static void insertion_sort(int[] arr, int first, int last, int gap)
{
int i, other, key;
for (i = first + gap; i < last; i += gap)
{
key = arr[i];
for (other = i - gap; other >= first && arr[other] > key; other -= gap)
{
{
arr[other + gap] = arr[other];
}
}
arr[other + gap] = key;
}
}
static void Main(String[] args)
{
int test_case = int.Parse(Console.ReadLine());
int[] arr = new int[test_case];
for (int i = 0; i < arr.Length; i++)
{
arr[i] = int.Parse(Console.ReadLine());
}
for (int gap = test_case / 2; gap > 0; gap /= 2)
{
gap = gap % 2 == 0 ? gap++ : gap;
for (int i = 0; i < gap; i++)
{
insertion_sort(arr, i, test_case, gap);
}
}
StringBuilder sb = new StringBuilder("");
foreach (int a in arr)
{
sb.AppendLine(a.ToString());
}
string output = sb.ToString();
Console.WriteLine(output);
}
}퀵 정렬( Quick sort )
퀵 정렬은 분할 및 정복 전략을 사용하여 배열 또는 목록을 정렬하는 정렬 알고리즘입니다. 이 알고리즘은 배열을 2개의 서브 배열로 분할함으로써 동작합니다. 하나는 선택한 피벗 값보다 작은 요소를 포함하고 다른 하나는 피벗 값보다 크거나 같은 요소를 포함합니다. 그런 다음 두 하위 배열 사이에 피벗 값이 배치됩니다.
분할 프로세스는 각 하위 배열에 이미 정렬된 요소가 하나만 포함될 때까지(즉 서브배열의 크기가 1이 될 때까지) 두 하위 배열에서 반복됩니다. 마지막으로 정렬된 서브어레이를 조합하여 정렬된 어레이를 형성합니다.
공간 복잡도는 일반적으로 O(log n)입니다. 이는 재귀 호출에 필요한 스택 메모리 때문입니다. 최악의 경우, 스택 메모리가 n만큼 필요할 수 있으므로 O(n)이 될 수도 있습니다.
최악의 경우(정렬되지 않은 경우에서 피벗이 항상 최소값 또는 최대값일 경우) 시간복잡도는 O(n^2)이 될 수 있습니다.
시간 복잡도: O(n log n) ~ O(n^2), 공간복잡도: O(log n)
퀵 정렬 알고리즘 작동원리
- 배열에서 피벗 요소를 선택합니다.
- 값이 피벗보다 작은 모든 요소가 피벗보다 앞에 오고 값이 더 큰 모든 요소가 피벗보다 뒤에 오도록 배열 순서를 변경합니다.
- 값이 작은 요소의 하위 배열에 동일한 단계를 반복 적용하고 값이 큰 요소의 하위 배열에 개별적으로 적용합니다.
퀵 정렬 알고리즘 예시
[ 6 , 7 , 4 , 8 , 9 , 1 , 2 , 5 ] 를 퀵 정렬한 예시입니다. (이때 피벗 값은 항상 배열의 첫번째 원소)

백준예제문제
2750번: 수 정렬하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
구현(실패)
쿽 정렬 알고리즘의 구현을 따라했지만 백준예제 문제에서는 실패함, 퀵정렬 알고리즘의 최악의 경우는 피벗이 항상 최소값이나 최대값으로 선택되는 경우에 발생합니다. 아마도 테스트 케이스 중에 퀵정렬 알고리즘이 최악의 경우가 되어 시간복잡도가(n^2)가 되어서 실패하는 듯 합니다.
//퀵정렬(시간초과 실패)
using System.Text;
using System.Diagnostics;
class MainApp
{
static void quick(int[] arr, int left, int right)
{
if (left == right)
return;
int pivot = left;
int low = left + 1;
int high = right;
while (low < high)
{
if (arr[low] <= arr[pivot])
{
low++;
}
if (arr[pivot] <= arr[high])
{
high--;
}
if (low < high && arr[low] > arr[pivot] && arr[pivot] > arr[high])
{
swap(ref arr[low], ref arr[high]);
low++;
high--;
}
}
if (arr[pivot] > arr[high])
{
swap(ref arr[pivot], ref arr[high]);
}
if (left != right)
{
quick(arr, left, high - 1);
quick(arr, low, right); ;
}
}
static void swap(ref int a, ref int b)
{
int sw = a;
a = b;
b = sw;
}
static void Main(String[] args)
{
int test_case = int.Parse(Console.ReadLine());
int[] arr = new int[test_case];
for (int i = 0; i < arr.Length; i++)
{
arr[i] = int.Parse(Console.ReadLine());
}
int left = 0;
int right = arr.Length - 1;
quick(arr, left, right);
StringBuilder sb = new StringBuilder("");
foreach (int a in arr)
{
sb.AppendLine(a.ToString());
}
string output = sb.ToString();
Console.WriteLine(output);
}
}힙 정렬
Heap Sort는 완전 이진 트리 자료 구조를 기반으로하는 정렬 알고리즘입니다. 이진 힙 자료 구조를 구성하고 그 구조에서 최대 또는 최소 값을 반복적으로 추출하여 정렬합니다.
힙 정렬 알고리즘의 시간 복잡도는 최악의 경우에도 일정한 시간복잡도를 유지합니다.
공간 복잡도는 입력 배열과 별도의 공간이 필요하지 않기 때문에 O(1)입니다. 즉, 정렬하고자 하는 배열의 크기에 상관없이 일정한 공간만 사용합니다.
시간 복잡도: O(nlogn), 공간복잡도: O(1)
힙 알고리즘 작동원리
- 주어진 배열을 최대 힙으로 구성합니다. 이 때, 부모 노드는 항상 자식 노드보다 큰 값을 가집니다.
- 최대 힙에서 루트 노드(최대값)를 추출하고, 추출된 값을 배열의 마지막 요소와 교환합니다.
- 배열에서 추출된 값을 제외하고 남은 부분을 다시 최대 힙으로 구성합니다.
- 2, 3 단계를 반복하여 정렬이 완료될 때까지 반복합니다.
힙 정렬 알고리즘 예시
힙 정렬에 대한 예시도 다음 블로그를 참고하였습니다.
[알고리즘] 힙 정렬(heap sort)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
구현
//힙 정렬(성공)
using System.Text;
class MainApp
{
static void swap(ref int a, ref int b)
{
int sw = a;
a = b;
b = sw;
}
static void Heapify(int[] arr, int n, int i)
{
int largest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < n && arr[l] > arr[largest])
{
largest = l;
}
if (r < n && arr[r] > arr[largest])
{
largest = r;
}
if (largest != i)
{
swap(ref arr[i], ref arr[largest]);
Heapify(arr, n, largest);
}
}
static void HeapSort(int[] arr)
{
int n = arr.Length;
for (int i = n / 2 - 1; i >= 0; i--)
{
Heapify(arr, n, i);
}
for (int i = n - 1; i >= 0; i--)
{
swap(ref arr[0], ref arr[i]);
Heapify(arr, i, 0);
}
}
static void Main(String[] args)
{
int test_case = int.Parse(Console.ReadLine());
int[] arr = new int[test_case];
int length = arr.Length - 1;
for (int i = 0; i < arr.Length; i++)
{
arr[i] = int.Parse(Console.ReadLine());
}
HeapSort(arr);
StringBuilder sb = new StringBuilder("");
foreach (int a in arr)
{
sb.AppendLine(a.ToString());
}
string output = sb.ToString();
Console.WriteLine(output);
}
}병합정렬(merge sort)
병합정렬(merge sort) 알고리즘은 분할 정복(divide and conquer) 방식을 사용하여 정렬하는 알고리즘 중 하나입니다.
공간 복잡도는 원래 배열의 크기와 동일한 크기의 추가 배열이 필요하므로, O(n)입니다.
각 부분 리스트는 더 이상 분할되지 않을 때까지 반으로 나누므로, 분할 단계에서는 O(log n)의 시간 복잡도가 소요됩니다. 각각의 부분 리스트를 정렬하고, 합병하는 단계에서는 각 부분 리스트의 크기 n에 비례하는 시간이 소요되므로, 이 단계의 시간 복잡도는 O(n)입니다.
시간 복잡도: O(n log n), 공간복잡도: O(n)
병합 정렬 알고리즘 작동원리
- 입력 배열을 가운데를 기준으로 두 개의 부분 배열로 분할합니다.
- 각각의 부분 배열을 재귀적으로 정렬합니다.
- 두 부분 배열을 병합(merge)합니다. 이때, 두 부분 배열을 비교하여 작은 원소부터 차례로 새로운 배열에 추가합니다.
- 모든 부분 배열들이 정렬될 때까지 이 과정을 반복합니다.
병합 정렬 알고리즘 예시
[5, 2, 8, 4, 1, 7, 6, 3]를 병합 정렬한 예시입니다.
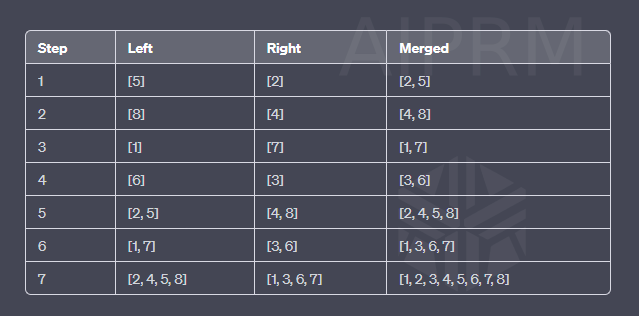
구현
//병합정렬 (성공)
using System.Text;
class MainApp
{
static void merge(int[] left, int[] right, int[] arr)
{
int num1 = 0;
int num2 = 0;
for (int i = 0; i < arr.Length; i++)
{
if (left.Length == num1)
{
arr[i] = right[num2++];
continue;
}
if (right.Length == num2)
{
arr[i] = left[num1++];
continue;
}
if (left[num1] < right[num2])
{
arr[i] = left[num1++];
}
else
{
arr[i] = right[num2++];
}
}
}
static void divide(int[] arr)
{
if (arr.Length <= 1)
{
return;
}
int len = arr.Length / 2;
int[] left = new int[len];
int[] right = new int[arr.Length - len];
for (int i = 0; i < left.Length; i++)
{
left[i] = arr[i];
}
for (int i = 0; i < right.Length; i++)
{
right[i] = arr[len + i];
}
divide(left);
divide(right);
merge(left, right, arr);
}
static void Main(String[] args)
{
int input = Int32.Parse(Console.ReadLine());
int[] arr = new int[input];
for (int i = 0; i < input; i++)
{
arr[i] = Int32.Parse(Console.ReadLine());
}
divide(arr);
StringBuilder sb = new StringBuilder("");
foreach (int a in arr)
{
sb.AppendLine(a.ToString());
}
string output = sb.ToString();
Console.WriteLine(output);
}
}시간복잡도가 O(nlogn)인 알고리즘들은 기본적으로 배열을 작은 배열로 나누어 정렬을한다. 그래서 함수와 재귀가 쓰이고 공간을 적게 사용할 수있다. 사실 위 코드들은 해당 알고리즘을 바탕으로 내가 직접 구현 하다보니 퀵 정렬 알고리즘 같이 최적화가 안되는 코드들이 몇개 있다.
'알고리즘' 카테고리의 다른 글
| 스택( stack )의 구현과 메소드 사용 [C#] (2) | 2023.04.18 |
|---|---|
| 큐( queue )의 구현과 메소드 사용 [C#] (0) | 2023.04.18 |
| 정렬 알고리즘 시간 복잡도, 공간 복잡도와 구현 (0) | 2023.04.05 |
| 유클리드 알고리즘 정의 (0) | 2023.03.31 |
| 브루트 포스 알고리즘 정의 (0) | 2023.03.21 |

